This project focuses on efficiently retrieving website information for all restaurants in New York City using the Google Places API. While NYC has a comprehensive database containing addresses and geographical coordinates for all its restaurants, it notably lacks website information. The goal is to collect website URIs for these known locations, which will later be scraped for menu data to populate a restaurant recommendation application.
Understanding the Challenge
To retrieve the website URI for each restaurant, you can make individual API calls using the business's name or address as parameters. However:
- Cost per call: $0.05.
- Total restaurants: ~30,000.
- Total cost: $1,500 for individual calls.
A more cost-effective approach is leveraging the Google Places Nearby Search API, which can return website URIs for up to 20 restaurants in a single call for the same cost of $0.05. This approach can reduce the total cost by up to 20x in the best-case scenario.
Methodology and Optimization Problem
The Google Places Nearby Search API provides results based on a given geographic coordinate, search radius, and place type (e.g., 'restaurant'). The problem is now framed as an optimization, with the objective of minimizing the number of API calls, subject to the constraint that every restaurant location is covered in the set of API calls.
The constraint requires each restaurant’s coordinates to fall within the radius of at least one Nearby Search call. This forms a geometric set cover problem: the goal is to cover all restaurant locations using the fewest circular regions (API calls), each with a maximum capacity of of 20 restaurants.
Overview of Workflow
1. Data Preparation
- Input: Raw NYC restaurant inspection database.
- Processing: Cleaning and standardizing geographic coordinates for all restaurant locations.
2. Geometric Coverage Optimization
- Approach: Solve the set cover problem using greedy and linear programming algorithms.
- Output: Generate circles (API call parameters) with variable radii and center coordinates.
3. Output File Generation
- Purpose: Create a blueprint for API calls.
- Contents: A file listing latitude, longitude, and radius for each API call.
Data Analysis and Visualizations
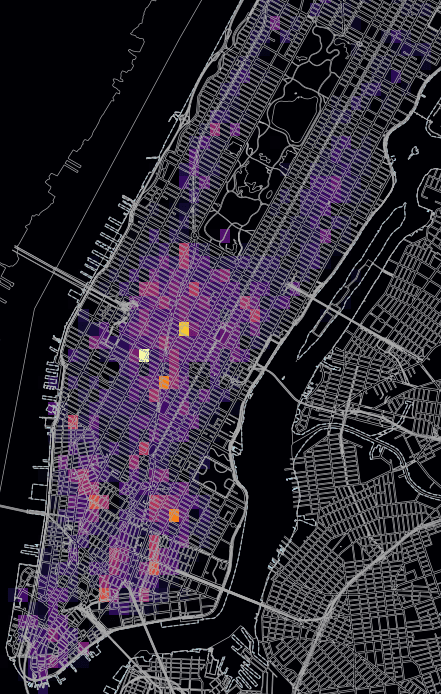
This section presents visualizations of the cleaned DOHMH NYC Restaurant Dataset highlighting the spatial distribution of restaurants across the city. The goal of these graphs is to inspire the development of covering algorithms by illustrating spatial relationships. The plots below include:
- Geographical Clustering (DBSCAN) Heat Maps: These identify areas with high restaurant density, making it easier to pinpoint highly concentrated zones.
- Voronoi Diagram: This depicts the spatial distribution of restaurants, with each cell representing an area of influence for individual restaurants.
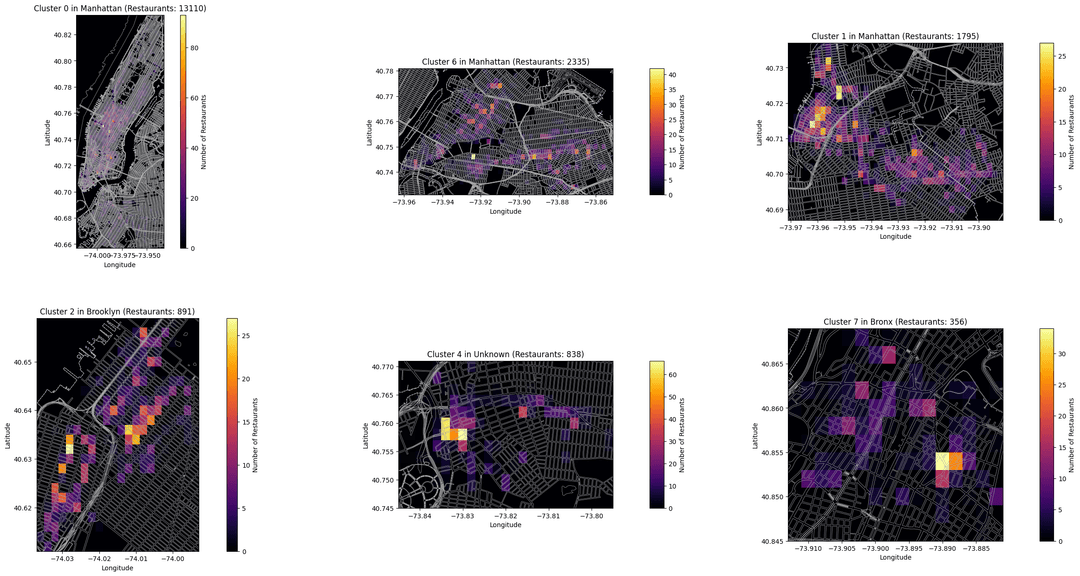
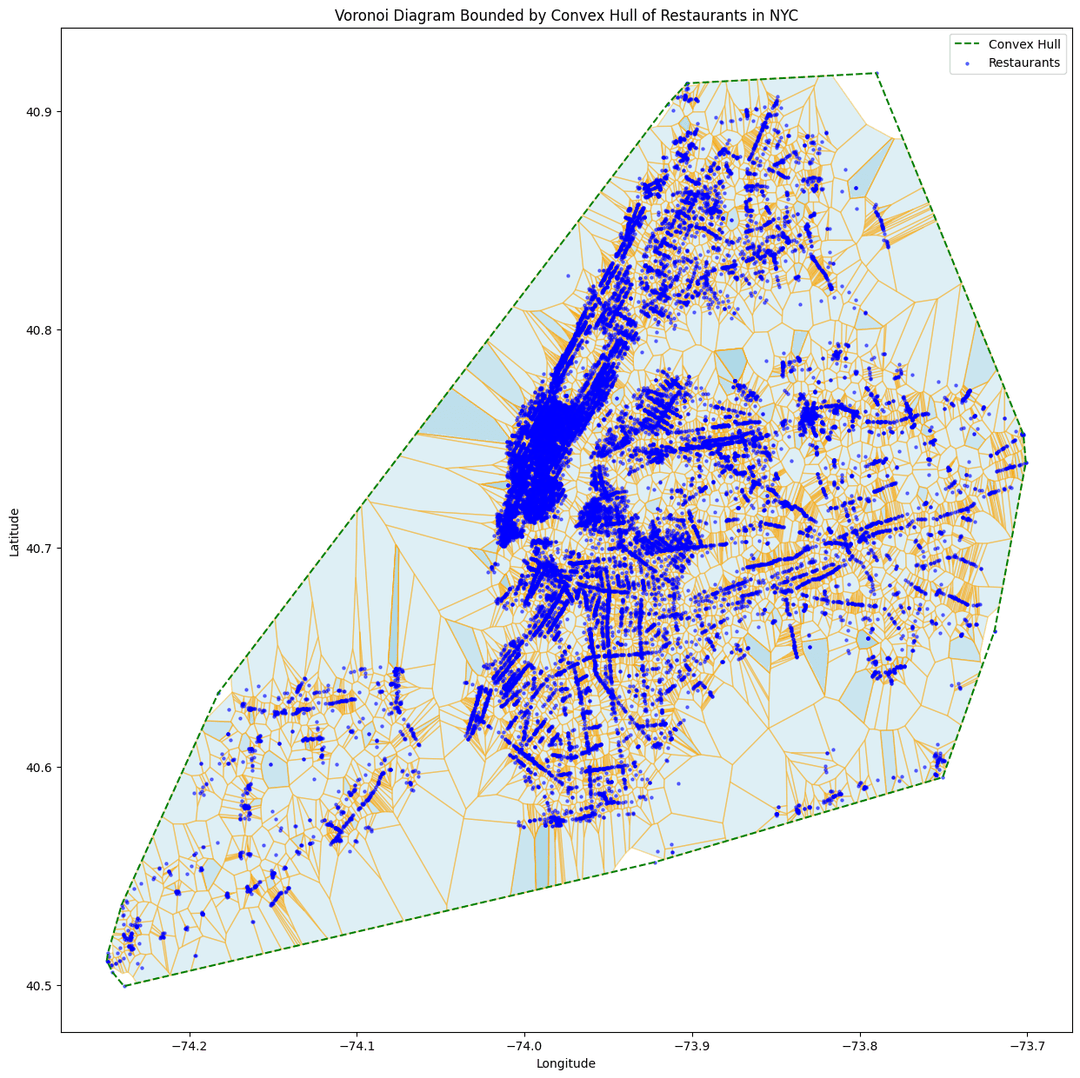
Covering Algorithms Implementation and Performance Metrics
Geometric Set Cover Problem with Disks
The geometric set cover problem involves selecting the smallest number of geometric shapes—specifically, disks—that collectively cover a given set of points in space. The objective is to find the smallest subset of these disks that covers all the points.
Generating the Initial Set of Disks
The following heuristic is used to generate the initial disk set:
- For each point in the dataset, generate a disk centered at that point.
- Assign to each disk a radius equal to the distance required to encompass the 20 nearest neighboring points.
This procedure ensures that every point lies within at least one disk. Although this approach guarantees complete coverage, it does not necessarily yield an optimal solution.
Optimization Strategies
To reduce the number of disks while maintaining complete coverage, two algorithmic strategies are considered:
-
Greedy Algorithm
- At each step, select the disk that covers the largest number of currently uncovered points.
- In the event of a tie, preference is given to the disk with the larger radius.
- The process is repeated until all points are covered.
-
Linear Programming Approach
- Utilize a multiplicative weighting method.
- Produces an ε-net, which serves as an approximate set cover with provable guarantees.
- Further optimization is possible by incorporating geometric properties of the disks; however, this would necessitate the use of geometric transformations, computational geometry libraries, and more complex spatial algorithms.
The size and time complexity of the greedy solution is acceptable with an approximately 10x total cost reduction from individual restaurant searches.
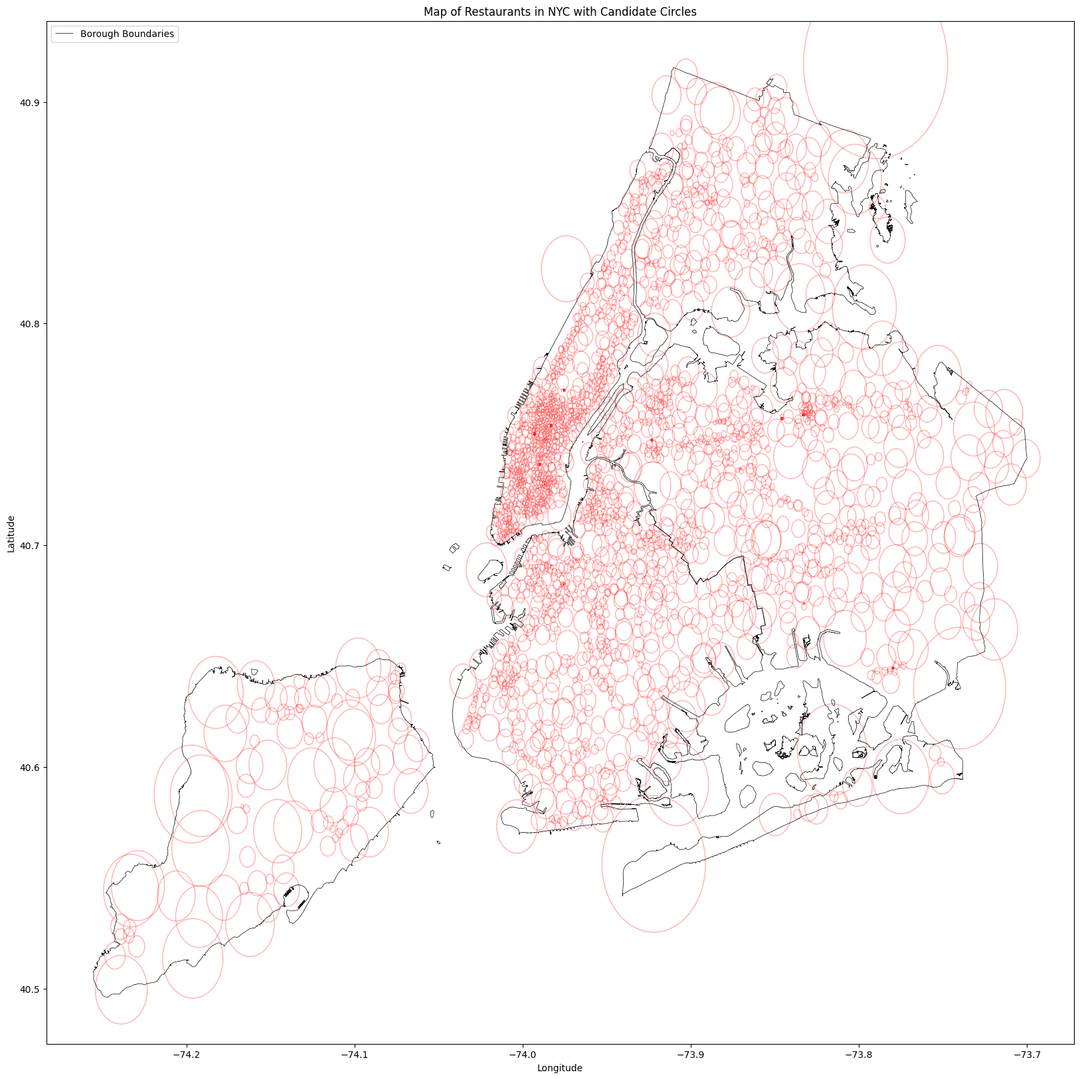
Visualizing the Result
The graph below shows the coverage of the selected circles and identifies overlapping regions that can be optimized through a more refined selection of candidate circles and the use of geospatial structures to strengthen the linear programming approach.
Conclusion
The greedy algorithm is the most intuitive algorithm and the solution produced is within a constant of less than two. Additionally, overlap between circles is not detrimental and can even enhance coverage, particularly in high-density locations. For future work, the highest-value improvement would be developing an algorithm to generate a larger set of candidate circles.
This blog post is based on my Jupyter Notebook that contains additional plots and a more detailed walk through.
Acknowledgments
Agarwal, P. K., & Pan, J. (2014). Near-Linear Algorithms for Geometric Hitting Sets and Set Covers. Annual Symposium on Computational Geometry - SOCG’14. doi:10.1145/2582112.2582152 Chan
Chan, T. M., & He, Q. (2020). Faster approximation algorithms for geometric set cover. CoRR, abs/2003.13420. https://arxiv.org/abs/2003.13420